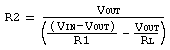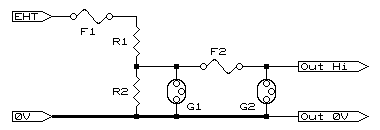
Measuring Voltages
in Excess of 1kV

Warning: This is not for the feint hearted. Voltages spoken of here are lethal and work must not be attempted by non-qualified personnel.

There are many times voltages of beyond 1kV need to be measured, but doing so safely requires a little engineering. Most times voltage transformers are employed (see Measuring beyond 230VAC) but there are times this is not practical, especially if VTs are not available at the voltages required, or simply prohibitively expensive.

A voltage divider is an apparent answer, and there is no apparent reason it shouldn't work. Imagine however, you calculate your voltage divider, you pop in a few resistors and every seems to be going well......

and the lights go out!

Now all would be well if this was your own home and all you've blown is the main incoming fuse. But you've not done this at home, you were trying to measure a major 3.3kV line at the main plant where you work and now the whole plant is dead! So, let's teach you what the books didn't.

Resistors have a breakdown voltage which is when the voltage between the windings exceeds the insulation between the windings. Even carbon and metal film are 'wound' on the former, the spiral shape created when the resistor is trimmed onto value during manufacture. Typical operating voltages of most commonly available resistors, which is both the voltage that may be across the resistor as well as between the resistor and its immediate surroundings, usually falls in the range of 250 to 500VAC for 1/4W and up. It is strongly advised that this be checked before using any type in high voltage applications.

There is effectively two issues to overcome:

1. Ensure the resistors can handle both the voltage across them and also safely dissipate the power asked of them.

2. If there should be a breakdown, the circuit will not allow a high voltage to appear at the measuring equipment.

Issue 1: There are two ways of tackling this, either employ special high voltage resistors, or create a chain from standard resistors. Caddock (www.caddock.com) are well known makers of high voltage resistors although they are a little pricey. Strings of standard resistors have one advantage over using high voltage alternatives being the resistance of the upper arm can be accurately created (usually a problem - see later).

With standard vs. high voltage, one needs to seriously weigh up the time spent building resistor chains with standard resistors costing a few pence as opposed to simply wiring in costly high voltage ones. The questions that need to be asked are whether or not the circuit demands a high level of safety, and if so then high voltage types are the only way to go. Please note that there are special handling precautions with high voltage resistors, please adhere to them (manufacturers usually supply instructions).

Calculating the resistors is fairly simple. For starters one should, for measurement purposes, not operate at lower then 1k-ohm/volt (i.e. 1meg/kV). This serves two purposes being:

1. the circuit does not put much drain on what is being measured (the drain possibly affecting readings if on a high impedance circuit) while maintaining a reasonably low output impedance so as to not lose any high frequency component, and,

2. the resistors don't get too warm!

If possible (and adhering to the 1meg/1kV rule), the value of R2 should be smaller than or equal to 1-tenth the impedance of the measuring instrument. This is not extremely critical especially if the instrument can be scaled, all that is required is to calculate the loading on the voltage divider. Formulae are shown below.

Divider Ratio (VIN : VOUT)	Divider Factor (VOUT / VIN)
Actual Voltage In	Actual Voltage Out
Finding R1 if R2 is fixed	Finding R2 if R1 is fixed

If you have chosen the route of building resistor chains then the formula for calculating the upper arm is also shown. This has the advantage of allowing you to build the exact resistance required. For example, we are measuring 3.3kV in and have 220V out (exact 11:1) and using the formula of 1meg/kV we have a lower leg of 220k. Our instrument has an input of 2meg meaning the actual resistor we use will be, using the standard formula for resistors in parallel, 1 ÷ ((1/220) - (1/2000)) = 247k. But 247k does not exist although we could create one using a 200k and 47k in series but this will still cause an error.

We'll opt for the next commonly available resistor being 270k bringing R2||RL to 237.9k. Using the formula to calculate R1 when R2 is fixed we determine the value required at 3330.6k. As we already bought a 270k the wise thing would be to buy a string of them and we land up using 12 of them with a 82k and 8.2k to make the desired chain. The costs are kept to a minimum while maintaining accuracy (yes, we did throw 400 ohms away but as that's only 0.012% we did not figure it important). Remember, this is an example and by no means the only values you can use.

One last very important figure that requires calculation is the power being dissipated in each resistor. This is calculated by working out the voltage across each resistor and then applying the formula P = V² ÷ R where V is the voltage and R the resistance. It is strongly suggested that a safety factor of at least two be built in i.e. should the dissipated power be 250mW then ½watt resistors be employed.

Issue 2: Should you suffer a breakdown i.e. the resistors flash over, then F2, G1, and G2 come into their own. Their one and only purpose is to ensure the primary measured voltage is not presented to the instrument. The way this is done is when the voltage exceeds the firing voltage of G2 it starts to conduct. If this was during a breakdown i.e. a lot of current is available, then F2 will blow. If G1 was not there then the full whack of the input voltage would be across a fuse not capable of breaking such a voltage. G1 ensures this cannot happen by keeping the voltage across F2 to a reasonable level (it is still recommended that 'sand-filled' safety fuses are used).

G1 and G2 are capable of 20kA fault currents for short periods and therefore rely on a decent fault path (shown by the bold line in the diagram), please provide one. Please also note that 0V means zero volts i.e. Ground. It is not always possible (mainly due to cost) to have F1 being a fuse with a voltage rating of about twice the measured voltage. However, a suitable alternative is a very thin piece of wire stretched over about 2cm/kV measured. G2 should be at least 1.5 times the measured voltage (especially at AC) with G1 about the same again. For 200V output suggested values are a 350V gas tube for G2 and 600V for G1.

During construction of such a voltage divider always ensure all parts have adequate clearances for the voltages being measured. It's all very well having made resistor chains with no more than 250V across each resistor, and then lying the circuit against a metal chassis while trying to inject 3.3kV or so (unless you like man-made lightning!).

Improved Safety: This may come as a small surprise, but using this type of voltage divider improves safety. First, the voltages being taken to the instrument are now at a far safer potential than the incoming voltages. Insulation on the test leads becomes far less critical. Second, and most importantly, there are no high currents available on the test points. Should the leads, by accident, come in contact with earth (hey!, it's very easy to clamp the leads in a cabinet door), then the amount of current is limited to the input volts divided by the upper resistor value. The resistor may get a little warmer, but that is the only 'damage' done (as well as having to re-do the measurement!).

For 3-phase measurements you will need to construct 3 such circuits, all using Ground as a reference point (0V). Please do not try to operate this circuit phase-to-phase as the 0V point will now be at phase potential. There are two dangers, the first being the 0V side will no longer have any current limiting, and the voltage into the instrument will more than likely be beyond the breakdown voltage of the instrument (apologies for stating the obvious, but there are those that would try this!).

Please approach this with every ounce of caution you can muster, and happy measuring!